
Introduction
When trying to figure out the Power Density of different batteries and fuel sources, the resources encountered both on the web and in scientific papers seemed confused. Definitions were presented in terms of power per unit volume, power per unit mass, some even unique measures like in terms of volume per unit time.
Which is correct? I explore this question in this article.
Foundational Knowledge
Let’s begin with something foundational and likely more familiar to the general reader: Energy Density (more familiar) and Specific Energy (less familiar). If you are already familiar with these metrics, feel free to skip straight to the Power Density section.
Energy Density
Energy Density is defined as energy per unit volume. It represents the energy stored in a given system or region of space per unit volume. This can be represented by the following equation:
Energy Density = Energy / Volume
where,
- Energy is usually measured in joules (J) or watt-hours (Wh)
- Volume is usually measured in liters (L)
Note that 3,600 joules equate to 1 watt-hour.
This means that Energy Density can measured in terms of J/L or Wh/L, with their attendant 1,000 factorisations, like MJ/L or MWh/L.
Energy Density is an important metric when we are trying to maximise the amount of energy that can be stored within a system or region, while trying to minimise the size of the space that region needs to be. For example, when working with batteries for mobile phones, energy density would be an important metric if we were concerned with phone ergonomics – maximising the amount of battery capacity available, while reducing the size (and hence bulkiness) of the device, something pursued by phone manufacturers as highlighted in this study.
Energy Density is often confused as being measured in terms of unit mass. One example of this is on the Clean Energy Institute website, which claims that li-ion batteries have energy densities approaching 300 Wh/kg. Though this value may not be in dispute, calling the metric “energy density” is wrong. Instead, energy measured per unit mass is represented by a different metric: Specific Energy.
Specific Energy
If we wish to define energy in unit mass terms, for example in J/kg or Wh/kg, we would instead rely on the metric of Specific Energy. It’s equation is as follows:
Specific Energy = Energy / Mass
where,
- Energy is usually measured in joules (J) or watt-hours (Wh)
- Mass is usually measured in kilograms (kg)
Admittedly, this is a rather unintuitive name, which might explain the confusion in the preference for popular literature to substitute out Specific Energy for Energy Density wherever possible.
Specific energy is important when the mass of a system is an important factor. One of the fields where this is crucial is that of transportation, where we would prefer higher specific energy fuels. Such fuels allow the carrying of less fuel for the same amount of energy required, saving on the costs of transporting the extra fuel.
With our foundational understanding of Energy Density and Specific Energy, we can now turn to the metric of Power Density.
Power Density
We can try understand Power Density in the context of Energy Density, because both have such similar units. Where Energy Density looks at energy per unit volume, Power Density looks at energy flow per unit volume. By energy flow, we mean power, which is energy per unit time. The equation below defines Power Density:
Power Density = Power / Volume
where,
- Power is usually measured in watts (W), but could also be in joules per second (J/s)
- Volume is usually measured in liters (L)
Based on the equation, we can see that Power Density represents how much power a given volume of something can supply.
Wait a minute. Volume of something?
What is this something?
To answer this question context matters.
Volume when looking at combustible fuels
In the context of combustible fuels, the Power Density of a fuel allows us to determine how much of a fuel to burn, to get a specific output of Power, like so:
Power = Power Density of Fuel x Volume
Here, Power is not measured in watts (which generally applies only to electrical power), but rather in J/s. In general, the greater the volume of fuel, the greater the power.
This is why when we want a bonfire to burn brighter on Guy Fawkes night, we throw in more wood. Because wood generally burns at the same Power Density (controlled for factors like species of tree, surface area exposed for exothermic reaction with oxygen, weather conditions, etc), we know that putting more wood in the fire increases its power output.
Volume when looking at batteries
Bigger batteries don’t always mean more power, so it seems like power density might be a moot metric, since we can’t fix it at a constant.
We can work another angle however. In general parlance, batteries have 3 levels of abstraction: battery cell, battery, and battery bank. One or more cells, form a battery. Two or more batteries arranged in parallel form a battery bank. Fun fact: This also explains why some batteries are marketed as “single-celled batteries.”
Production at each level of these abstractions is usually standardised, which means that the specifications of a battery cell, battery or even battery bank are constant factors under tested conditions – including Voltage (V), Amperage (A) and Volume of the product (V).
We know that Power can be computed with Voltage and Amperage, like so:
P = VI
This allows us to derive a Power Density constant of a battery cell, battery or battery bank, by combining the above with our power density equation.
Power Density = Power / Volume of Battery Product
Power Density = VI / Volume of Battery Product
Can we think of uses for such a value?
Perhaps we could use it to estimate the volume a battery would need to be to link up a certain number of battery cells, that will enable it to satisfy a given amount of power output; knowing this theoretical constraint could help us design more efficient or smaller batteries.
We could also use our the computed Power Density constant to plan required real estate purchases for a grid-scale battery bank project; if we know the vertical height allowances of the project, or the stacking limit of the battery banks, we could theoretically estimate the land area we would need for such a project.
Interestingly, we can stretch definitions by stating that volume doesn’t even need to be in terms of liters (L) or even an SI unit. It could just be in terms of any unit that represents size.
We could even size it in terms of camels, like this asteroid was. Wasn’t this line of thinking how they came up with the Imperial system with its feet and yards and chains in the first place? On second thought, maybe let’s not go there.
Volume when looking at combustion engines
So far, we have looked at Power Density for energy storage mediums, like fuel and batteries. But just to show how broad of a view volume can take, let’s have a look at combustion engines.
Computing a Power Density for a fuel tank wouldn’t make any sense. Not only does the fuel stored in the tank need to be reacted on to produce energy, how fast that reaction happens also doesn’t depend on the fuel tank itself. Rather, how fast we convert the fuel into power depends on the combustion engine. That’s why some studies on combustion energy define power density as the ratio of power to the maximum specific volume in the cycle of the engine.
In this case, Power Density looks at the relationship between the amount of power released by a combustion engine, against how large it is. If an engine can be engineered to have higher Power Density, we would be able to design smaller, less bulkier engines for vehicles. This could enable more space for other purposes, like larger fuel tanks for longer range, or smaller cars with better aerodynamics without sacrificing storage or passenger space.
Crucially, power output is not constant in engines, dependent on factors like the amount of fuel being pumped into it. Anyone who has driven a car might intuitively understand this, having used an accelerator to vary the amount of fuel fed to their engine. This is likely why car engines are measured and marketed with engine displacement as a metric (in cc), alongside others. In general, the higher the displacement, the larger the power, scaled approximately along Power Density lines of the kind of technology used for the engine.
So far we have seen that our choice of the volume independent variable depends on what we are trying achieve, and nowhere will that be clearer than in our next section, where we present a very interesting and useful version of Power Density.
Surface Power Density
Volume doesn’t even need to be in terms of liters (L) or even an SI unit. It could just be in terms of any unit that represents size.
Remember how we mentioned the above earlier? Surface power density takes this up (or down?) a notch, by representing our metric not in terms of volume, but in terms of area. This metric represents the electrical power produced per horizontal surface area, which is a metric that makes a useful comparator for different forms of energy production. Some examples for perspective:
- Wind: where stacking up wind turbines wouldn’t make any sense.
- Solar: where stacking up solar cells also wouldn’t make any sense.
- Biofuels: where the land area is measured not in generator size but in crop land, where stacking up crops on cropland wouldn’t make any sense.
These examples show how we can use surface power density to compare between different configurations of energy production, to find the most cost-effective or efficient means of production. This is in fact, what this linked study does, comparing between 9 different types of energy generation including wind, solar, biofuels and even managing to rope in coal and nuclear.
The height dimension doesn’t vary the final power output in any of the 3 cases above, and so it makes sense to disregard it and simply use area as the denominator.
Power Density is not always a useful metric
What if we looked at the context of a hydroelectric dam?
If we measure the Power Density of the hydroelectric dam in terms of the volume of the dam, what happens if we somehow manage to double the volume of the dam, maybe by joining it up with an adjacent valley through a tunnel? Ceteris paribus, that mean that our Power Density halves… but so what? Our dam turbines are still turning out power at the same rate, while the amount of energy we can now store has effectively doubled.
In this case then, Power Density as a metric doesn’t bring any particularly useful inference. All we know is that we can double the number of active turbines in our setup to bring Power Density back in line. But we would be better served measuring power demand or energy storage in days, which are certainly more useful operational metrics.
In such scenarios, and others like it, computing Power Density can be redundant.
Context matters
The crucial thing here is this: when gauging the independent volume variable for Power Density, context matters. We have to first understand the source or topic we are looking at, before applying the equation. Blindly applying the equation might have us computing a useless metric like the power densities of engine based on the volume of their fuel tanks (possible, but pointless), or power densites for dams (also possible, and also pointless).
In fact, personally I would even suggest that context matters in all the other metrics we have mentioned so far, especially given the very prevalent mixing up of all the mentioned metrics with each other.
One last metric: Specific Power
Like how Specific Energy is energy in terms of mass, Specific Power is power in terms of mass. It measures the amount of power provided by a power source, per unit of mass.
Specific Power = Power / Mass
We can also see this in terms of the parellel between Energy Density and Specific Energy. Density for volume, specific for mass.
The resolution for our earlier problem
We saw earlier that a search for Power Density of different products produced conflicting definitions.
For example, Power Density in terms of mass is cited in these studies: Applications of high power density lithium ion batteries and A Low-Cost, High Energy-Density Lead Acid Battery.
This one study, Lead/acid batteries, even defines the power density of lead-acid batteries in terms of area.
In Design Fundamentals of High Power Density, Pulsed Discharge, Lead Acid Batteries, Specific Power is used to describe power in terms of mass.
Note that this confusion is not limited to Power Density and Specific Power. It applies also in the case of Energy Density and Specific Energy, as in the paper Li-ion batteries: basics, progress, and challenges, by Da Deng, which defines Energy Density in both Wh/L and Wh/kg.
These are just a small sample, there are numerous other cases providing conflicting definitions.
As such, it does seem like the definition of Power Density provided above requires a certain amount of proof, since it does not seem to be a widely accepted view.
Rabbit hole
To get to the bottom of this for everyone (but mostly to sate my own nagging curiousity), I did a dive into the rabbit hole of Google search and academic journals and publications, and came across 2 foundational sources that seem to support my view.
The first is a technical guide, Guide to understanding battery specifications, from the Massachusetts Institute of Technology, or MIT. This guide lists out a series of battery metrics, with our 4 metrics laid out one after the other.
The second is a book by Professor Emeritus Vaclav Smil, from the University of Manitoba, whose interdisciplinary research (taken directly from his website) deals with interactions of “energy, environmental and population change, food production, history of technical innovation, risk assessment, and public policy.” Emphasis mine. His book Power Density: A Key to Understanding Energy Sources and Uses lays out that
In SI terms, power density is a derived unit measured in J/m³, but in energy publications this density is often expressed (with the exception of gases) in mass terms as MJ/kg or GJ/t. This may be a cause for confusion because in SI nomenclature, J/kg is a derived unit called specific energy.
Two relatively authoritative sources that support our view.
Yet the smoking gun to me was our concept of Specific Power, discussed above. To me, the fact that we had Specific Power` as a definition out there in the wild, that specifically (pun unintended) was intended (pun intended?) to define a power / mass relationship in energy studies made everything fall into place for me. In fact, our 4 metrics including specific power, fit a very neat quadrant.
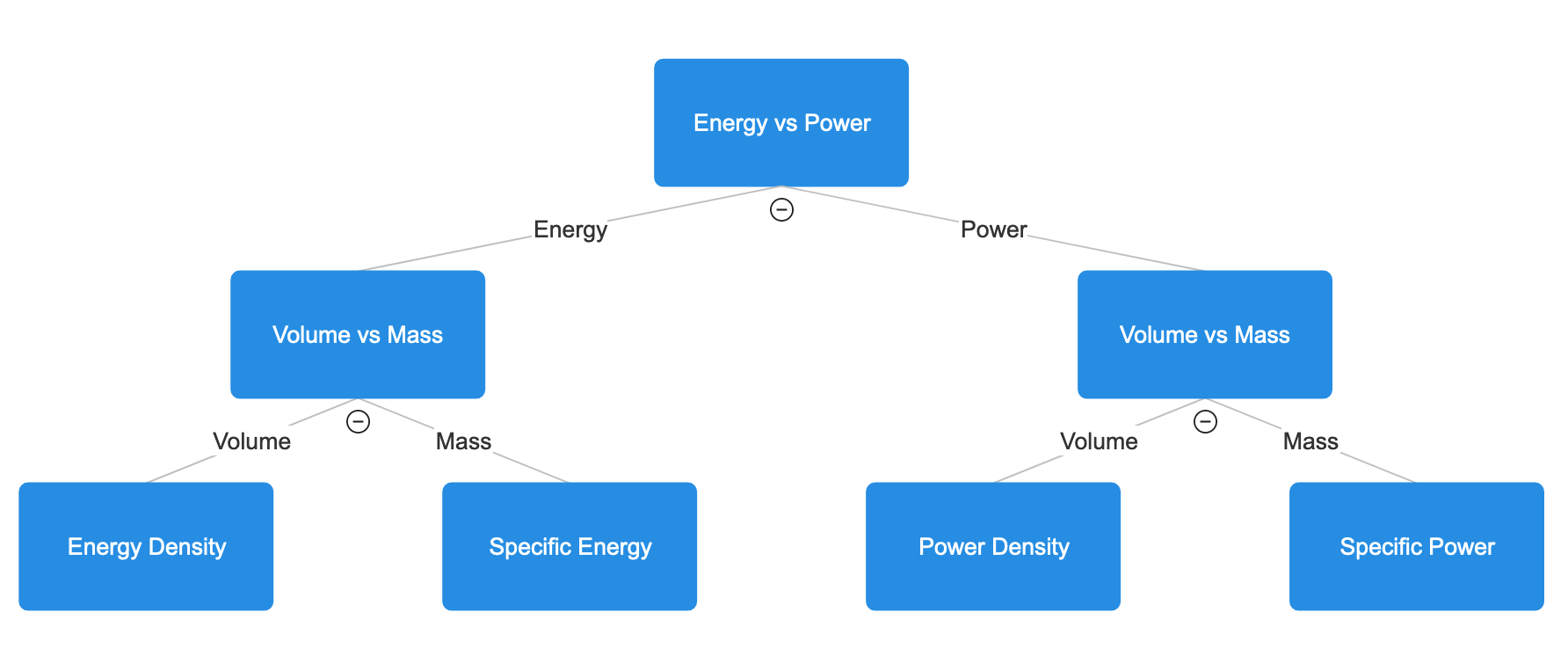
The Quadrant
We can arrange our 4 metrics of energy density, specific energy, power density and specific power very neatly in a quadrant, with the headers of (a) energy vs power, and (b) volume vs mass:
| Energy | Power | |
|---|---|---|
| Volume | Energy Density | Power Density |
| Mass | Specific Energy | Specific Power |
This table is not only useful in helping us understand the relationship between the four metrics, but also in helping us to decide which metrics are most useful for application to different use cases.
We can do this by applying the next two questions.
Is energy or power more important?
We can rephrase the above – do we care more about the cost-effectiveness of a power source in storing a lot of energy for a long period of time, or more about the cost-effectiveness of a power source in releasing a lot of energy over a short period of time. If the former is more important, prioritise the metrics along the energy dimension. If the latter, prioritise the metrics along the power dimension.
Take for example the difference between wood and charcoal.
Both have equivalent energy densities, but charcoal has a better ability to release energy very quickly, allowing the achievement of the high levels of temperature needed to liquify slag in many ancient copper smelting operations. Something I learned from years of watching Primitive Technologies on YouTube. So one would choose a fuel source with a high Power Density or Specific Power in this case, rather than worrying too much about Energy Density or Specific Energy.
Is volume or mass more important?
Here, we are concerned with how much space something takes up, versus how much it weighs.
If space is the premium, maybe in city centres where real estate is more expensive, then we worry more about volume. If the weight of something matters more, perhaps in use cases where we need to carry the power source wherever we go (like fuel for a cargo plane), then the mass will be what we are more concerned with.
Decision tree
Though not the biggest fan of decision trees, some people do find them helpful. So here’s what the above considerations would look like visually:
Remember that Context Matters
The misconceptions are understandable given how density can simply refer to how much of something there is in something else. By definition, it needs to be in terms of volume, but colloquailly we can see how we can refer to it in any way.
In certain cases, this distinction is not even important. For example, if freshwater is used as the medium, then both kg and L are equivalent in a practical sense, since 1 liter of water weighs exactly 1 kilogram at standard gravitational acceleration.
Understandably, this can be frustrating to learners or practioners, especially if one does a search for Power Density, but all results seem to return specifications of machinery / tools / products that are based on Specific Power instead.
But we can’t really get authors to correct their papers because of definitional wrongs. What we can do however is understand the distinction between the different metrics, and pay attention to the unit of measure, regardless of what the author calls it. We can (and should) also pay attention to the purpose and context of the metric being used.
We might take it a step further, and be more skeptical toward papers or resources that mix up their usage of such metrics – imprecise definitions might reflect a lower attention to detail, imprecise experiment methodology or misconceptions that could affect the quality of the knowledge produced.
Even then, articles and papers with some imprecisions can arguably still be useful on the whole. No one is perfect after all.
Hope this helps :)